Wie kann man schnell und einfach die Zahlen von 1 bis 100 addieren? Ist die Zahl
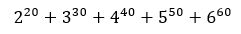
durch 7 teilbar? Und was passiert, wenn man ganz viele Reiskörner auf einem Schachbrett stapelt?
Mit Fragen wie diesen setzen sich seit Schuljahresbeginn zwölf Schüler*innen in der AG „Mathe für die Uni“ jeden Freitag nach der sechsten Stunde unter der Leitung von Stefan Tassemeier und Tobias Tegelkamp auseinander.
Die Schüler*innen erlernen in der AG das formal korrekte Aufschreiben von mathematischen Aussagen, z.B. durch Summenzeichen, Mengensymbolen und Kongruenzen. Diese Schreibweisen werden genutzt, um neue mathematische Beziehungen zu erforschen und erste eigene Beweise zu führen. So konnten die Teilnehmenden z.B. bereits die Summenformel
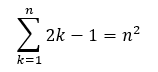
selbstständig entdecken und beweisen, indem sie auf die berühmte Summenformel des kleinen Gauß zurückgegriffen haben. Stefan Tassemeier, der die AG als Student während seines Praktikums am Pascal mitgestaltet, ergänzt die mathematischen Inhalte dabei immer wieder durch interessante Hintergrundinformationen aus dem Studium. Bemerkenswert ist auch die Zusammensetzung der AG: Sowohl ein Schüler aus der Klasse 7 als auch verschiedene Schüler*innen aus den Jahrgangsstufen EF, Q1 und Q2 sind Woche für Woche motiviert dabei – sogar eine weitere Lehrkraft hat schon einmal die AG besucht. Alle Beteiligten scheuen sich dabei nicht, auch schwierigere Probleme anzugehen, wie z.B. den Beweis der Summenformel
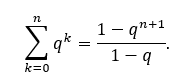
Doch die Mühe lohnt sich! Nicht selten hört man nach einer Phase intensiven Nachdenkens ein glückseliges „Aaaaahhh, das kürzt sich ja weg!“. Besonders schön sind auch die Momente, in denen die Mathematik der eigenen Intuition einen Streich spielt. So konnten wir in der AG mithilfe der obigen Summenformel beweisen, dass die Gleichung
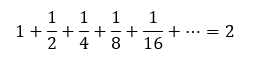
gilt oder dass 0,999… exakt die gleiche Zahl ist wie 1. Bis zu den Ferien setzen sich die Teilnehmenden der AG nun mit Fragen der Teilbarkeit auseinander und haben dazu mit vielen Zahlenbeispielen die Grundlagen der modulo-Rechnung erkundet. Unter Ausnutzung des kleinen Satzes von Fermat, der eine sehr starke Aussage über das Verhalten von Potenzen beim Teilen durch Primzahlen aussagt, konnte ganz ohne Taschenrechner gezeigt werden, dass die Summe der großen Potenzen oben tatsächlich durch 7 teilbar ist. Ein Ausblick auf mathematische Verschlüsselungsverfahren wird die derzeitige Themenreihe abrunden und auch deutlich machen, dass Mathematik hier eine sehr wichtige Anwendung in der Realität hat.
Ein Einstieg in die AG ist grundsätzlich auch jetzt noch möglich. Nach jedem Treffen wird – ebenfalls sehr studiumsnahe – ein LaTeX-Skript erstellt, sodass die bisherigen Untersuchungen jederzeit zur Verfügung stehen. Interessierte und mathematikbegeisterte Schüler*innen können sich bei Fragen gerne an Tobias Tegelkamp wenden.

